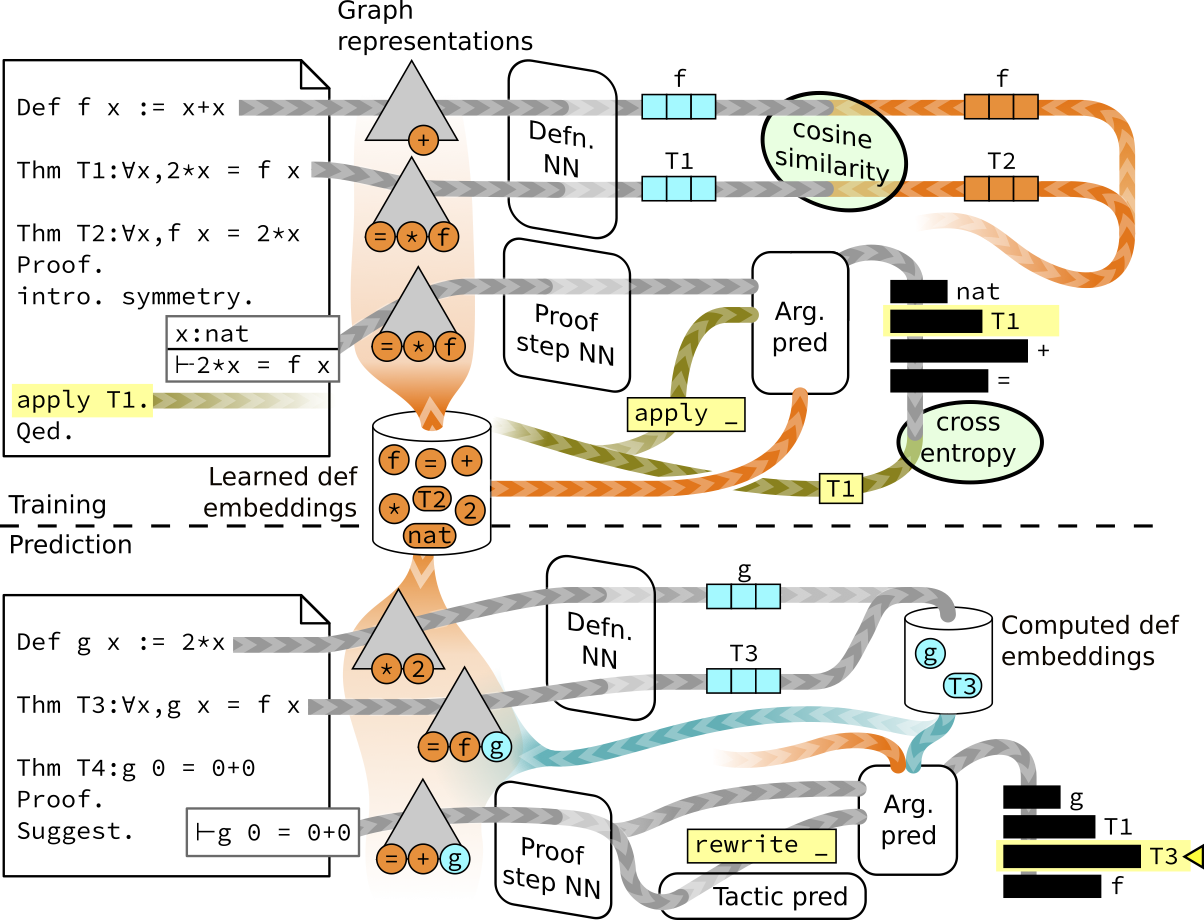
Graph2Tac is a novel neural network architecture for predicting appropriate tactics for proof states. The crucial innovation of Graph2Tac is that it can build an understanding of the math concepts in an entire Coq development and all of its dependencies on-the-fly. That is, it analyzes the structure of definitions and lemmas and builds an internal representation of each object in the global context. Then, when presented with a proof state that references these mathematical concepts, Graph2Tac can leverage its deep knowledge to predict tactics and arguments.
Text2Tac is a language model for synthesizing tactics. It receives the current proof state as a human-readable prompt and “completes” this prompt by synthesizing a tactic.
Comparison in capabilities of Graph2Tac, Text2Tac and Tactician’s default k-NN model:
- Representations: Graph2Tac is the only model that has deep background knowledge of the mathematical concepts in a library. Text2Tac and k-NN are informed only by the current proof state. References to objects in the global context are not resolved.
- Tactic prediction: All three models predict tactics in different ways,
with unique advantages and disadvantages.
- Text2Tac is capable, at least in principle, of generating completely free-form tactic expressions. However, because it has no knowledge of the tactics and lemmas currently available in Coq, it is forced to “hallucinate” tactics.
- Graph2Tac, takes a more structured approach in generating tactics. It first
chooses a “base” tactic, without any arguments, from a pre-defined set. For
example,
apply _. Then, it predicts an argument for each “hole” in the tactic. Arguments are pointers into the knowledge graph given to the model. Therefore, arguments are always valid objects. A downside is that Graph2Tac is unable to synthesize arbitrary terms as arguments. It is also incapable of leveraging previously unseen tactics defined by users. - The k-NN model sees tactics and their arguments as a black box. It is only capable of predicting the exact tactic and argument combinations that already exist in its database. However, this model is capable of learning from previous proof scripts on-the-fly. This is rather powerful in practice, because it can learn to use new user-defined tactics and can “borrow” script fragments from similar proofs defined close-by.
- Speed: The k-NN model is two order of magnitude faster than Graph2Tac, which in turn is an order of magnitude faster than Text2Tac.
Below is an overview of how Graph2Tac is trained to create definition embeddings and predict tactics and arguments. See the paper for more information on the architecture and performance of these models.
Installation
Graph2Tac and Text2Tac are proving agents implemented in Python. It is highly recommended that you use a virtual environment or conda environment to install them.
Graph2Tac is compatible with Python 3.9-3.11, while Text2Tac is compatible with Python 3.9-3.10. Install one (or both) of the agents using:
pip install graph2tac==1.0.4
pip install text2tac==1.0.1
Make sure that whenever you start Coq, the virtualenv where you made the
installation is available in your PATH.
Pre-trained models compatible with these agents are available in the Opam
packages coq-graph2tac and coq-text2tac. These packages contain all
configuration details needed to make Tactician interface with the agents. For
installation Opam >= 2.1 is recommended. Opam will prompt you to install Cap’n
Proto and XXHash through you system package manager. If your
system does not readily provide these packages, please consult the
prerequisites
page on Github for alternatives.
Make sure that you have an Opam switch available with the Coq repositories available. For example, you can create one as follows:
opam switch create tactician ocaml-base-compiler.4.11.2 --repos=custom-archive=git+https://github.com/LasseBlaauwbroek/custom-archive.git,coq-released=https://coq.inria.fr/opam/released,default
(This command includes the custom-archive repo, which contains some bugfixes
for Coq. This is optional. Note for MacOS: On MacOS, you will encounter bugs
with ocaml-base-compiler.4.11.2. You must use ocaml-base-compiler.4.12.1.
Then run either one of these commands (you cannot run both; coq-graph2tac and
coq-text2tac are mutually incompatible).
opam install coq-graph2tac coq-tactician-stdlib
opam install coq-text2tac coq-tactician-stdlib
If you which to instrument packages beyond Coq’s stdlib, the following command will inject Tactician in Opam’s compilation process. You can then install additional packages as normal.
tactician inject
Usage
Whenever you perform any command-line actions that involve Coq while you wish to
use Graph2Tac or Text2Tac, you have to prefix those commands with tactician exec. This will ensure that everything is loaded correctly. For example, you do
this when starting your editor or when building a project using dune or
make:
tactician exec -- coqc ...
tactician exec -- coqide ...
tactician exec -- make ...
tactician exec -- dune build ...
tactician exec -- emacs ...
Usage of Graph2Tac and Text2Tac is similar to the usage of Tactician’s default
model. You can ask the model for Suggestions and ask it to synthesize
proofs. More detailed descriptions of Tactician’s tactics are commands are in
the manual.
There is one important additional command to use. Tactician’s API synchronizes Coq’s entire global context with the external agent when it starts a proof search. This can be an expensive operation. However, it is possible to introduce cache points in a document, where the global context is proactively synchronized with the agent. After a cache point, only new items in the global context need to be synchronized. This greatly speeds up initialization of a prediction. Creating a cache point is done using
Tactician Neural Cache.
Alternatively, you can automatically create new cache points after every new Coq command using the option
Set Tactician Autocache.
Example
Start CoqIDE through tactician exec coqide, and try the following example:
From Tactician Require Import Ltac1.
(* Set Tactician to automatically introduce external caching points *)
Set Tactician Neural Autocache.
Inductive mynat : Set :=
| my0 : mynat
| myS : mynat -> mynat.
Fixpoint myadd n m :=
match n with
| my0 => m
| myS n => myS (n + m)
end where "n + m" := (myadd n m).
Lemma my_comm : forall n m, n + m = m + n.
Proof.
(* Commutativity requires three separate inductions.
That is too much. But Graph2Tac can do the inductions separately.
Text2Tac cannot. *)
induction n.
- synth.
- synth.
Qed.